连续形式 链接到标题

无需多言,公式就这么简单 $$ out(t)=K_p\left(e(t)+\frac{1}{T_i}\int_{0}^te(t)dt+T_d\frac{de(t)}{dt} \right) $$ 或者也可以写成三个系数的形式 $$ out(t)=K_pe(t)+K_i\frac{1}{T_i}\int_{0}^te(t)dt+K_d\frac{de(t)}{dt} $$ 下面从各个项解释一下

比例项 链接到标题

看看纯比例项的PID $$ out(t)=K_pe(t) $$

• 可以理解为信号与系统里面的无记忆(与过去无关)因果(与未来无关)系统，输出仅取决于当前时刻的误差
• $K_p$越大，系统响应越快，但是超调也会随之增加(严重的话会产生不可忽略的震荡)
• 存在不可忽略的稳态误差($K_p$越大稳态误差越小)

稳态误差可以理解为这一种“趋势”(比如摩擦力)与驱动力的动态平衡，比如

• 在控速PID中显然会一直受到摩擦力的作用，使得最终控诉结果会小于预期值
• 在锅炉控温时自然散热这种降温的“趋势”也造成了实控温度会变低 因此最后稳态误差偏向于“趋势”的方式

通过两张图片可以很好的理解稳态误差

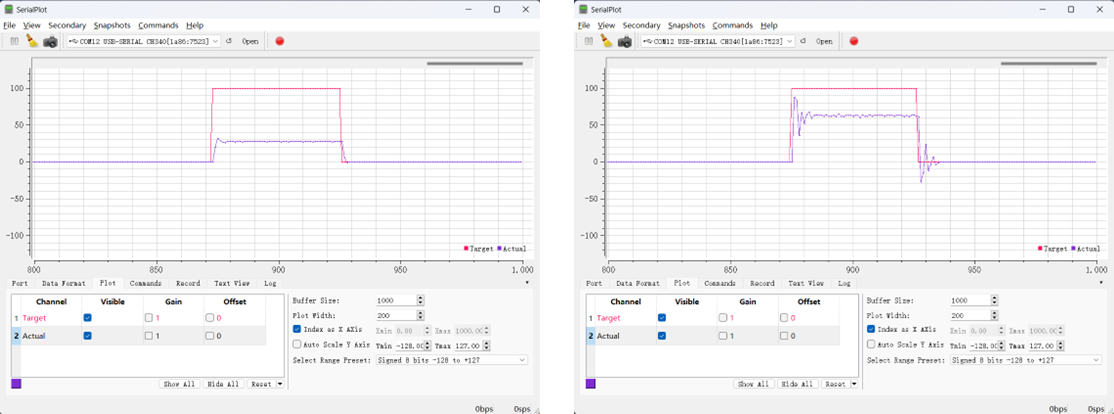
左边的是$K_p$较小的时候,右边是$K_p$较大的时候，

积分项 链接到标题

• 积分项还取决于历史时刻
• 从理解上来看，也就是说只要有误差存在，积分项就会随时间一直增大，从而务必会使得误差为零才罢休，因此这也就很能弥补稳态误差了。
• $K_i$越大，积分项权重越大，稳态误差小时越快，但是也就有更强的滞后性(原理和$k_P$大的原因相同)

微分项 链接到标题

前面无论是纯比例项还是加上了积分项，在$K_p,K_i$很大的时候都会“冲”，即越过预期值，并可能在预期值附近反复震荡，恶性的话甚至会变成自激振荡，最后凭空产生误差。微分项的原理就是使得实际值在快被调回时减速，从而让实际值在接近目标值时稳定下来。

离散形式 链接到标题

……