微分先行 链接到标题

针对情况 链接到标题

当目标值在短时间内发生较大变化时，微分项会产生较大的干扰，导致系统不稳定.因此，我们可以考虑将微分项放在前面，即先行微分。

一个很简单的例子就是应对阶跃响应时候I项在跳变点会趋于无穷(很大)。

可视化小调整 链接到标题

单独观察微分项DifOut，做实验，可以发现单独只有微分项的情况也能实现调整，不过显然是不能完全调到目标值的，有点类似于切割磁感线的效果(然而D本来的目的只是阻尼作用，并不能调整)。

代码实现 链接到标题

因此，所谓的微分先行就是直接发挥其阻尼作用——取实际值的微分，而不是再依赖误差的微分。 实现代码就是更改微分项即可

DifOut=-Kd*(Actual-Actual1);

但是实际上这个更改非常具有个性化，要具体情况具体分析。比如有的时候不微分先行反而是好的(P和D共同调控)

不完全微分 链接到标题

  • 传感器的噪声会被微分项放大，产生抖动甚至自激振荡。(噪声对D项的影响是最大的)
  • 所谓的不完全微分想要实现的是一个低通滤波器的效果(给微分项加入一阶惯性单元)，
    • 优点：使得波形更平滑；
    • 缺点：响应速度变慢，系统的动态性能下降。(一定会有延后，理解就是取100个取平均值肯定比10个取平均值要延后) 如果直接给代码的离散形式的话还是有点难理解的，那么我们先从连续形式取理解

理解 链接到标题

我们知道，对于正常PID系统，其连续形式如下 $$ u(t)=K_p e(t)+K_i \int_0^t e(\tau) d\tau+K_d \frac{de(t)}{dt} $$ 那么不完全微分就是这样 $$ u(t)=K_p e(t)+K_i \int_0^t e(\tau) d\tau+K_d \frac{e(t)-e(t-\tau)}{\tau} $$ 看起来好像变成了差分的形式？对！这就是他要的效果，虽然在实际使用中使用的是离散的形式，但是P、I、D的时间分度值都是一样的，也就是PID调控的周期，这里通过$\tau$这个参数的引入，使得对于微分的时间分度值与PI分离了，可以在保证PI精度的同时自主控制$\tau$实现我们想要的滤波程度。

代码实现 链接到标题

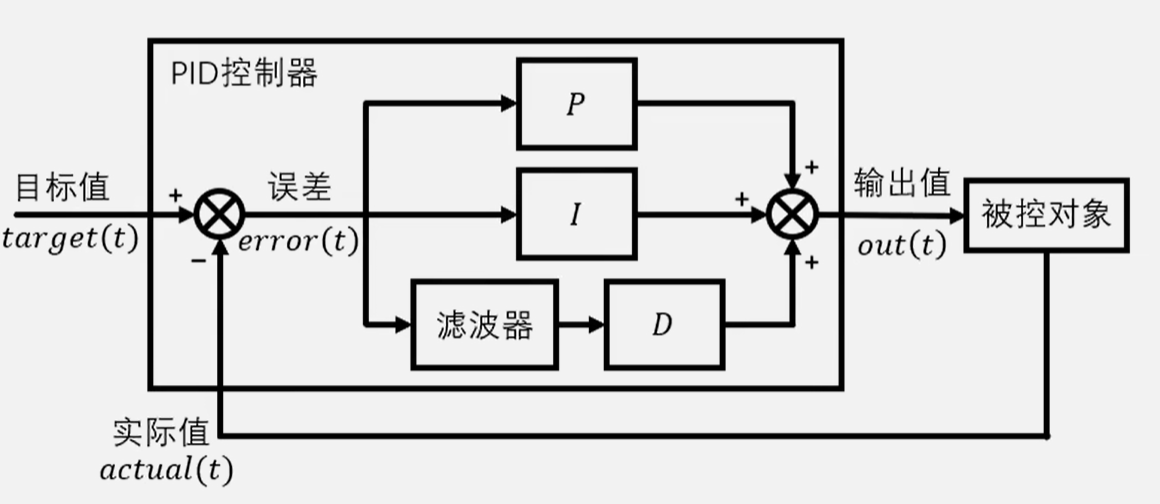
但是我觉得他在代码上的实现和我再连续角度理解的有所出入，他对微分项是这样改的 $$ DifOut(k)=(1-\alpha)K_d(err(k)-err(k-1))+\alpha DifOut(k-1) $$ 意思是当前的微分项输出是当前的微分结果与上一次微分结果的一个加权和， 下面给一个系统框图增进理解 alt text

当然，也可以将输入滤波改为输出滤波。

实操 链接到标题

  • 按照上面的公式修改DifOut，并在串口输出中增加输出；
  • 使用C语言自带的随机数生成器生成初始微扰抖动
    • 首先需要添加头文件
#include <stdlib.h>
  • 然后加入下面命令对Actual进行扰动
Actual+=rand()% 41-20; // 产生-20到20的随机数

不加入不完全微分的结果 链接到标题

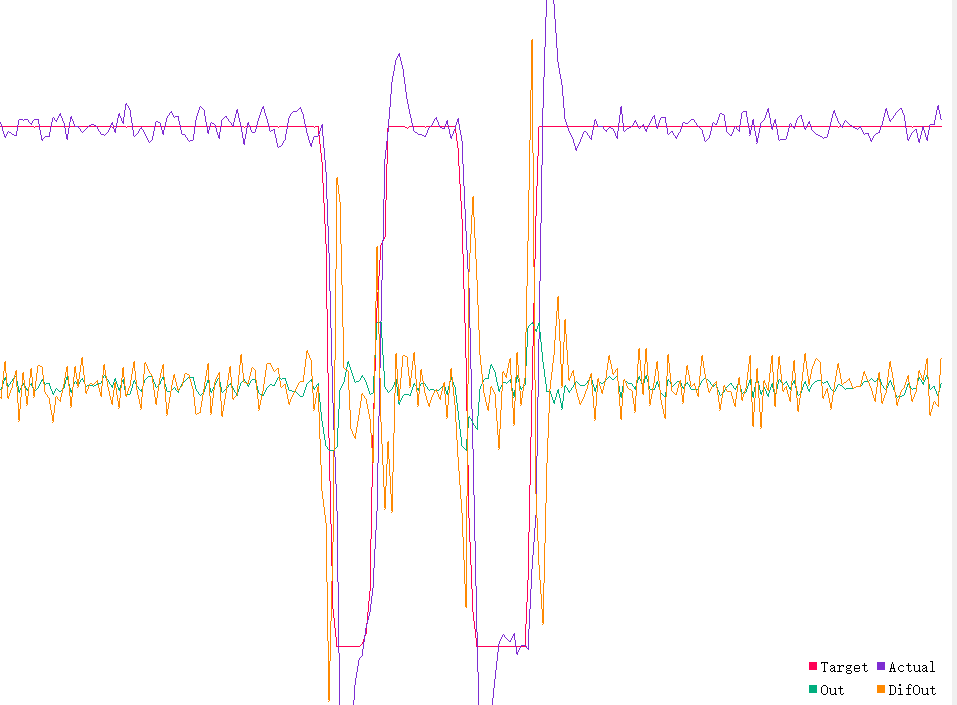alt text 可以看到DifOut在目标值迅速变化时的波动非常大，

引入不完全微分 链接到标题 

DifOut=a*Kd*(Actual-Actual1)+(1-a)*DifOut;

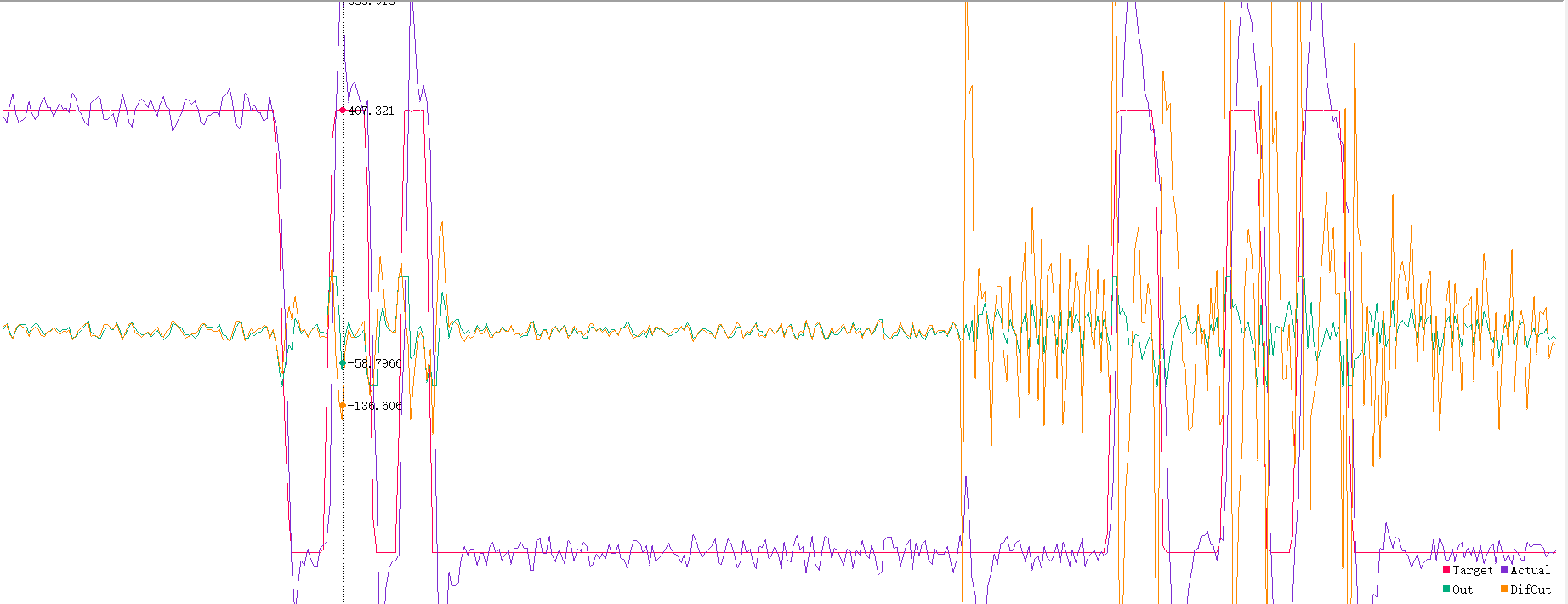alt text 前面一段是a=0.1，后面一段是a=0.9的情况，可以看到随着a的减小，DifOut的波动也减小了。